TinyMPC项目的github代码链接为https://github.com/TinyMPC/TinyMPC。

下图分别展示了TinyMPC动态避障和8字跟随性能以及火箭软着陆问题上的轨迹跟踪性能试验。

（1）动态避障

TinyMPC 的运行速度足够快，可以在每个时间步骤重新线性化约束，使其能够推理移动的障碍。在左侧，以棒末端为中心的虚拟球在每个时间步骤中被线性化为一组新的超平面约束。该算法还可以处理任意数量的任意线性约束。例如，在右侧，它在yz平面中避开棒末端。

（2）“8”字跟踪

对比了相同的库存控制器，以完成一个不可行的快速数字8跟踪任务（只有当无人机更强大时，才能满足完成单个数字8的时间）。TinyMPC和PID能够保持直立，但TinyMPC的轨迹更接近数字8。

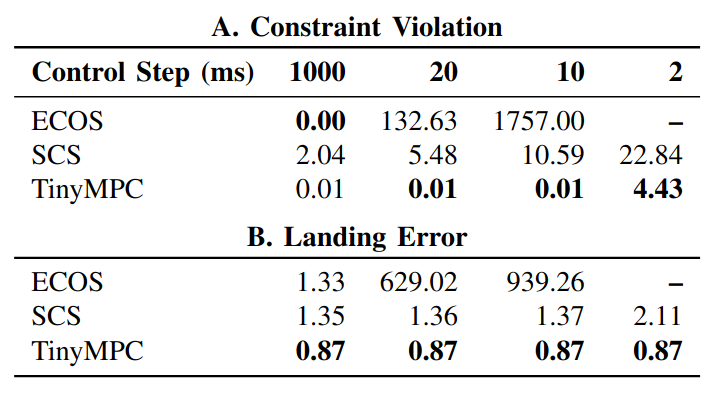
（3）实时控制需要一个求解器在一个严格的时间窗口内返回一个解。比较了TinyMPC在火箭软着陆问题上的轨迹跟踪性能，同时人为地改变每个解可用的时间量。在所有控制持续时间内，TinyMPC比SCS和ECOS违反约束更少，跟踪误差更小。

1摘要

模型预测控制（MPC）是一个强大的工具，以控制高度动态的机器人系统的复杂约束。然而，MPC对计算要求很高，而且通常无法在小型、资源有限的小型机器人平台上实现。我们提出了TinyMPC，一种高速MPC解算器，具有低内存占用，针对小型机器人上常见的微控制器。我们的方法是基于乘子的交替方向法（ADMM），并利用MPC问题的结构来提高效率。我们通过对最先进的求解器OSQP进行基准测试，证明了TinyMPC的有效性，实现了近一个数量级的速度增长，以及通过在27克四旋翼上的硬件实验，证明了高速轨迹跟踪和动态避障。TinyMPC可以在https://tinympc.org上公开获得。

2简介

模型预测控制 (MPC) 可实现机器人的反应式动态在线控制，同时考虑复杂的控制和状态约束，例如动态避障和接触事件期间遇到的约束 [1]、[2]、[3]、[4]。然而，尽管 MPC 取得了许多成功，但其实际应用往往受到计算限制的阻碍，这可能需要算法简化 [5]、[6]。在处理具有快速或不稳定开环动态的系统时，这一挑战会更加严重，因为这些系统需要高控制率才能安全有效地运行。

与此同时，人们对可在密闭空间内操作的微型低成本机器人的兴趣激增，使其成为从紧急搜索和救援 [7] 到基础设施和设备的日常监控和维护 [8]、[9] 等应用的有希望的解决方案。这些机器人的计算仅限于低功耗、资源受限的微控制器 (MCU) [10]、[11]。如图 2 所示，与大型机器人上的 CPU 和 GPU 相比，这些微控制器的 RAM、闪存和处理器速度要少几个数量级，而且过去无法支持计算密集型或内存密集型算法的实时执行 [12]、[13]。因此，文献中许多在这些微型平台上执行的智能机器人行为示例都依赖于机外计算机 [14]、[15]、[16]、[17]、[18]、[19]、[20]。

近年来，出现了几种适用于嵌入式 MPC [29]、[30] 的高效优化求解器，最著名的是 OSQP [31] 和 CVXGEN [32]。这两个求解器都具有代码生成工具，使用户能够创建无依赖性的 C 代码来在嵌入式计算机上求解二次规划 (QP)。然而，它们没有充分利用 MPC 问题的独特结构，通常导致它们占用过多的内存并且计算要求过高，无法在许多微控制器的资源限制内运行。

另一方面，“TinyML”最近的成功使神经网络在[12]微控制器上的部署成为可能。基于这些结果，我们开发了TinyMPC，这是一种使用乘子（ADMM）的交替方向算法优化的凸MPC优化实现。在其核心，我们的求解器是通过利用MPC问题的结构来加速和压缩ADMM算法。

图1 TinyMPC是一种快速凸模型预测控制求解器，可以对资源受限的微控制器进行实时最优控制。我们在27克的裂缝四旋翼上证明了它在动态避障（上）和恢复90◦姿态误差（下）方面的有效性。

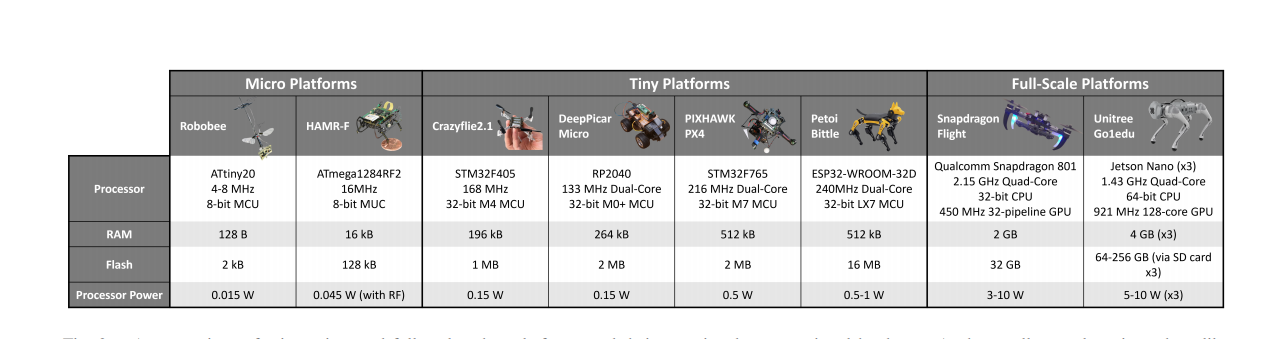图2 微型、微型和全尺寸机器人平台及其相关计算硬件的比较。在最小的规模上，像机器人蜂[21]和HAMR-F [22]这样的微型机器人使用高度受限的8位微控制器来执行预先计划的开环步态或机翼运动。在大规模飞机上，骁龙飞行四旋翼[23]或联合部队Go1edu四足动物[24]上拥有强大的嵌入式cpu和gpu，可以以高功率需求为代价实现高性能。在这项工作中，我们的目标是微型机器人，如疯狂的2.1[25]，深度芯片微型[26]，像素鹰PX4 [27]，和Petoi Bittle [28]，利用32位微控制器进行运动规划和控制。这些设备能够进行一些板载计算，但在处理器速度、内存和闪存方面比全尺寸机器人要低几个数量级。

特别是，我们预计算和缓存昂贵的矩阵分解，允许TinyMPC完全避免在线除法和矩阵求逆。这种方法能够以非常小的内存占用进行快速计算，从而能够部署在资源受限的mcu上。据作者所知，TinyMPC是第一个为这些mcu上执行定制的MPC求解器，该求解器已在一个高度动态、计算受限的机器人系统上演示。我们的贡献包括：

• 一种新的二次规划算法，它为MPC进行了优化，是无矩阵反演的，并实现了高效率和非常低的内存占用。这种组合使它适合于部署在资源受限的微控制器上。

• 是C++中的TinyMPC的开源实现，为微控制器上的凸MPC问题提供了最先进的实时性能。

• 在一个小型、敏捷、资源受限的四旋翼平台上的实验演示。

本文继续进行如下：第二节回顾了线性二次最优控制、凸优化和ADMM。第三节然后推导出核心的TinyMPC求解器算法。第四节介绍了裂缝四旋翼飞机的基准测试结果和硬件实验。最后，我们在第五节中总结了我们的结果和结论。

3背景

A.线性-二次调节器（LQR）

[33]是一种广泛用于求解机器人控制问题的方法。LQR根据一组线性动力学约束条件优化了一个二次代价函数：

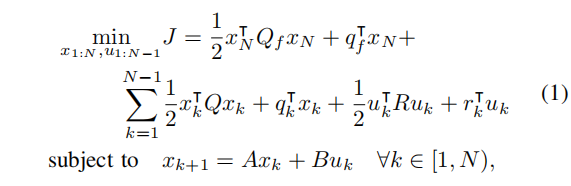
xk∈Rn，uk∈Rm状态和控制输入时间步k，N是时间步数（也称为范围），∈Rn×n和B∈Rn×定义系统动力学，Q⪰0，R≻0，Qf⪰0对称成本矩阵和q和r线性成本向量。

式(1)具有仿射反馈控制器[33]形式的封闭解：

反馈增益Kk和前馈dk是通过时间向后求解离散黎卡蒂方程，从PN = Qf，pN = qf开始，其中Pk，pk是代价（或值）函数[33]的二次项和线性项：

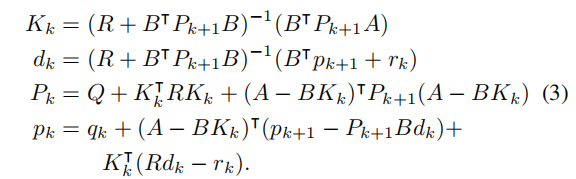
B.凸模型-预测控制

凸MPC扩展了LQR公式，允许对系统状态和控制输入有额外的凸约束，如关节和转矩极限、避障的超平面和接触约束：

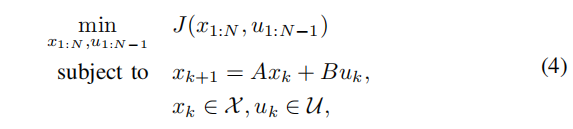
其中X和U是凸集。这个问题的凸性意味着它可以有效可靠地解决，使实时部署在各种控制应用，包括火箭的着陆[34]、腿运动[35]和自动驾驶[36]。

当X和U可以表示为线性约束时，(4)是一个QP，可以放为标准形式：

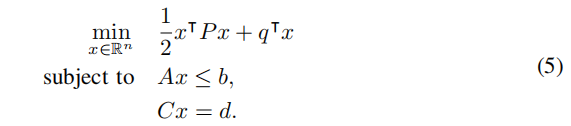
进一步的分析，包括可行性和稳定性可以在[37]和[38]的理论保证。

C.乘子交替方向法乘子交替方向法

（ADMM）[39]，[40]，[41]是一种求解凸优化问题的流行而有效的方法，包括qp，如(5)。我们在这里提供一个非常简短的总结，并参考读者到[42]了解更多细节。给定一个通用问题：

利用f和C凸，我们定义了集合C的指标函数：

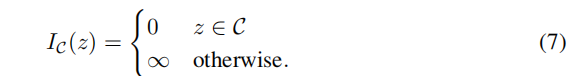
我们现在可以通过引入松弛变量z来形成以下等价问题：

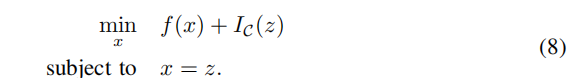
变换问题(8)的增广拉格朗日量如下，其中λ为拉格朗日乘子，ρ为标量惩罚权值：

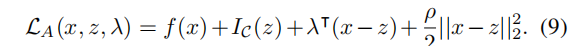
如果我们在x和z上交替最小化，而不是同时在两者上最小化，我们就得到了三步长的ADMM迭代，

最后一步是对拉格朗日乘子[41]的梯度上升更新。这些步骤可以被迭代，直到达到一个期望的收敛公差。

在QP的特殊情况下，ADMM算法的每一步都变得非常简单地计算：原始更新是一个线性系统的解，而松弛更新是一个线性投影。基于ADMM的QP求解器，如OSQP [31]，已经展示了最先进的结果。

4 TINYMPC求解

TinyMPC利用MPC问题的特殊结构，以通用性换取速度。具体来说，我们利用LQR问题的封闭形式的黎卡蒂解来计算（10）中的原始更新。预计算和缓存这个解决方案允许我们避免在线矩阵分解，并在实现非常快速的性能的同时保持较小的内存占用。

A.结合MPC的LQR和ADMM

我们解决了以下问题，引入了(9)中的松弛变量，并将(4)转换为以下变量：

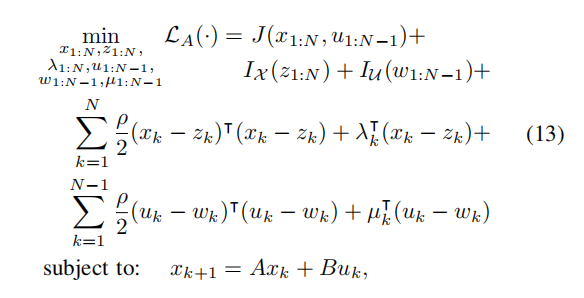
其中z，w，λ和µ是整个视界上的状态松弛、输入松弛、状态对偶和输入对偶变量。状态和输入约束通过指标函数IX和IU来强制执行。我们使用ADMM算法（10），（11），（12）来解决这个最优控制问题。（13）的原始更新成为一个相等约束的QP：

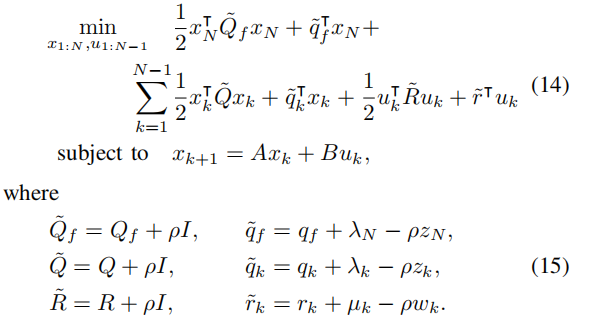
为了方便[41]，我们重新制定了（15），并引入了缩放的对偶变量y和g：

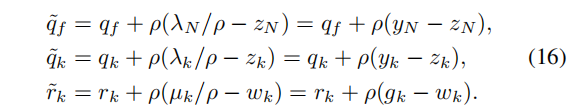
我们观察到，由于（14）表现出与(1)中相同的LQR问题结构，因此它可以通过(3)中的Riccati递归有效地求解。（13）的松弛更新变成可行集上的一个简单的线性投影：

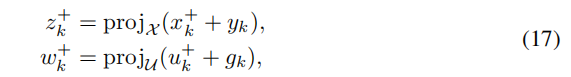
其中，上标表示后续ADMM迭代中的变量。（13）的双重更新变为：

最后，当原始残差和对偶残差在一个集合公差范围内时，该算法终止。

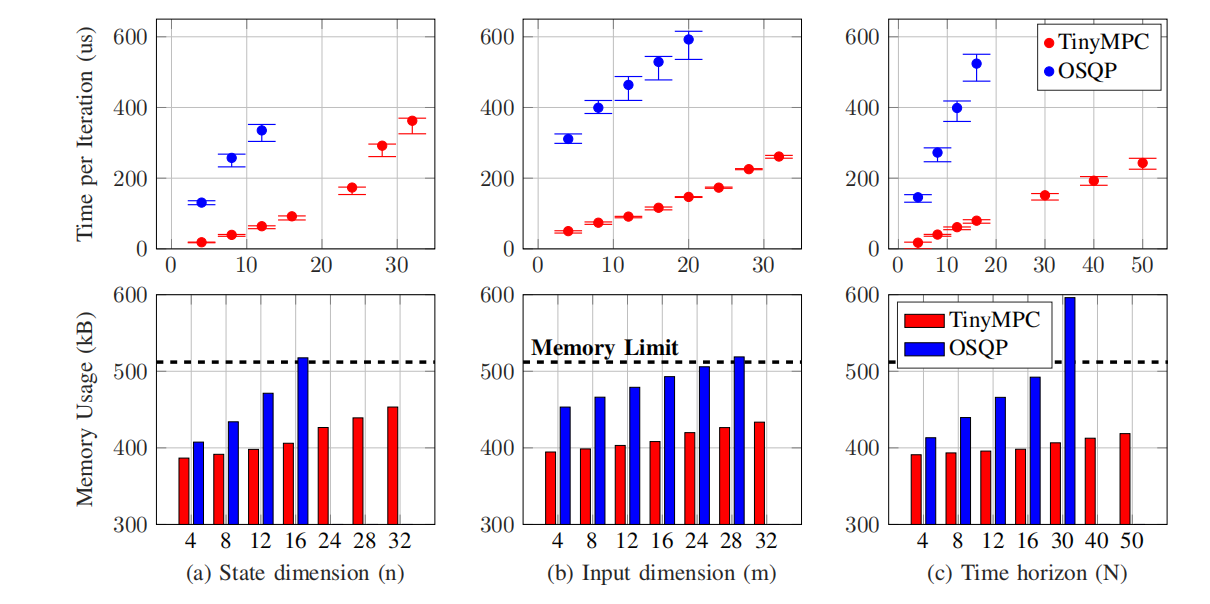
图3  比较OSQP和TinyMPC在Teensy 4.1开发板（ARM Cortex-M7运行在600MHz，32位浮点支持，7.75 MB闪存和512 kB紧密耦合RAM）上的平均迭代时间（顶部）和内存使用（底部）。错误条显示了针对给定问题执行的所有MPC步骤的每次迭代的最大时间和最小时间。在(a)中，输入维度和时间范围在m = 4和N = 10处保持不变，而状态维度n在4到32之间变化。在(b)中，n = 10和n = 10，而m在4到32之间变化。在(c)中，n = 10，m = 4和n从4到50不等。黑色虚线表示Teensy 4.1的内存限制

B.预计算

在每个原始更新中求解线性系统是每个ADMM迭代中最昂贵的步骤。在我们的例子中，这是黎卡蒂方程的解，它可以利用这些特性来显著减少计算和内存的使用。给定一个足够长的视界，黎卡蒂递归(3)收敛于无限视界LQR问题[33]的常数解。因此，我们预先计算一个LQR增益矩阵Kinf和成本去黑森Pinf。然后，我们从(3)中缓存以下矩阵：

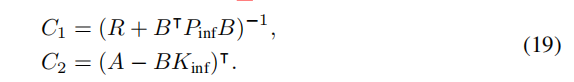
然后，对里卡蒂方程的仔细分析表明，只有线性项需要作为ADMM迭代的一部分进行更新：

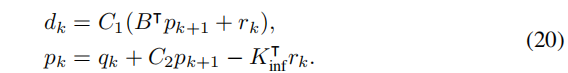
因此，我们完全避免了在线矩阵分解，只计算矩阵向量积。我们还通过在每个时间步长中只存储几个向量，大大减少了内存占用。

C.惩罚缩放

ADMM对(9)中的惩罚项ρ的值很敏感。像OSQP [31]这样的解决方案通过自适应地缩放ρ来克服了这个问题。然而，这需要执行额外的矩阵分解。为了避免这种情况，我们预先计算并缓存了一组对应于ρ的几个值的矩阵。

我们基于在OSQP改编的方案中的原残值和双残值在这些缓存矩阵之间切换。所得到的TinyMPC算法总结在算法1中。

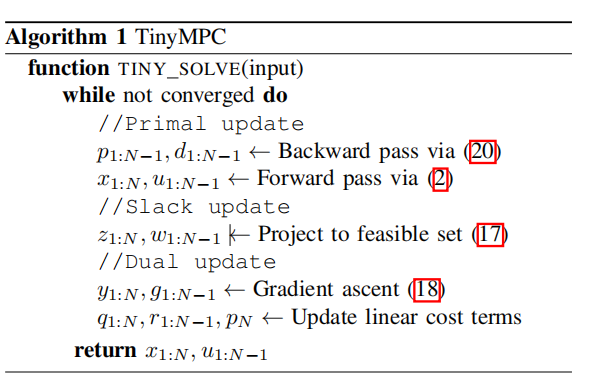
5实验

我们通过两组实验来评估TinyMPC：首先，我们将我们的求解器与一个具有代表性的微控制器上的最先进的OSQP [31]求解器进行基准测试，证明了改进的计算速度和减少的内存占用。然后，我们在资源受限的纳米四旋翼平台Crazyflie2.1上测试了我们的求解器的有效性。我们证明了TinyMPC使Crazyflie能够跟踪侵略性参考轨迹，同时满足控制极限和时变状态约束。

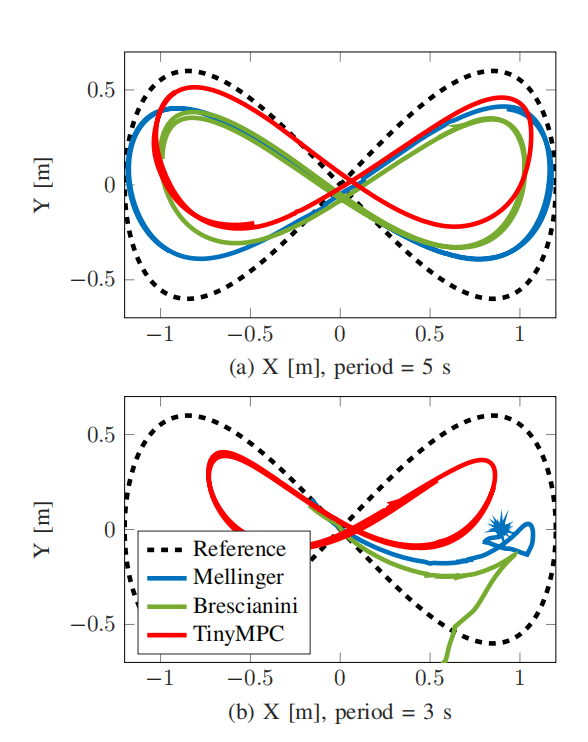图4  8字跟踪在低速（上）和高速（下）比较TinyMPC与Crazyflie上的两个性能最好的控制器。对于较慢的轨迹，所有三个控制器都具有相似的性能。对于更快的轨迹，只有TinyMPC能够保持跟踪而不崩溃。TinyMPC对悬停的最大速度和姿态偏差分别达到1.5 m/s和20。

A.微控制器基准

如图3所示，我们首先比较了TinyMPC和OSQP的随机线性MPC问题，同时改变了状态和输入维度，以及视界长度。

1)方法：实验在Teensy 4.1 [43]开发板上进行，该板有一个ARM Cortex-M7微控制器，工作在600 MHz，7.75 MB闪存和512kBRAM。TinyMPC是在C-++中使用特征矩阵库[44]实现的。我们使用OSQP的代码生成特性来生成一个要在微控制器上运行的每个问题的C实现。目标公差设置为10−3，约束公差设置为10−4。两个求解器的最大迭代次数都设置为4000，并且都使用了热启动。OSQP的溶液抛光被禁用以减少溶液时间。其他参数也被尽可能地设置为等效值。

随机生成动态模型A和B并进行检查，以确保状态维数n、输入维数m和时间视域n的所有值的可控性。控制输入被限制在整个视界的固定范围内。在微控制器测试中，添加了噪声来模拟不完全状态估计。最大的问题实例涉及696个决策变量，490个线性等式约束和392个线性不等式约束。

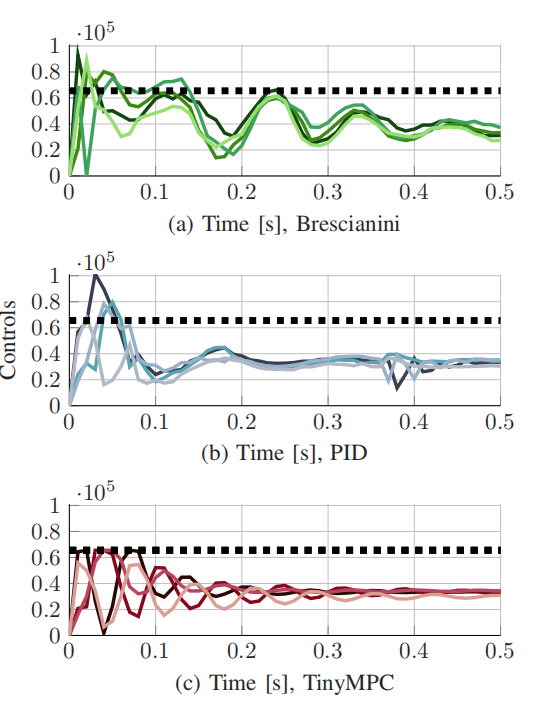
图5 极端初始姿态实验期间的控制轨迹。为每个控制器显示了四个预修剪的脉冲宽度调制电机命令。黑色虚线表示推力极限，从0到65535个脉冲宽度调制值。三个成功的控制算法中，只有TinyMPC可以解释控制可行性，展示了图1（底部）所示的机动。

2)评估：图3显示了两个求解器的平均执行时间，其中TinyMPC比OSQP的最大加速速度为8.85倍。这种加速允许TinyMPC在处理输入约束时执行实时轨迹跟踪。OSQP也很快超过了单片机的内存限制，而TinyMPC能够扩展到更大的问题规模。例如，对于固定的m = 4和N = 10的时间范围（图3a），OSQP超过了OSQP的n = 16的内存限制，而TinyMPC只在n = 32的状态维度下使用了约400 kB。

B.硬件实验

我们证明了我们的求解器在一个资源紧张的疯狂动物2.1四旋翼上实时执行动态控制任务的有效性。我们提出了三个实验：1)在缓慢和快速速度下的8字轨迹跟踪，2)从极端初始姿态恢复，3)通过在线更新状态约束的动态避障。

1)方法：Crazyflie 2.1是一个27克的象限。其主要MCU是ARM Cortex-M4（STM32F405），时钟频率为168 MHz，SRAM为192 kB，闪存为1 MB。OSQP无法容纳在此MCU上可用的内存中，因此无法用作MPC基线。相反，我们将与Crazyflie固件中包括的四个控制器Y[m]Y[m]控制进行比较：Cascaded PID[45]、Mellinger[46]、INDI[47]和Brescianini[48]。这些是反应控制器，通常会调整控制输入以满足硬件限制。

所有的实验都是在OptiTrack运动捕获环境中进行的，以100 Hz将姿势数据发送到疯狂动物。TinyMPC以500 Hz运行，水平长度为N = 15，用于图8跟踪任务和姿态恢复任务。对于避障任务，我们使用机载无线电将棍子末端的位置发送给裂缝虫。此外，我们将MPC频率降低到100 Hz，并将N增加到20。

在所有的实验中，我们线性化了四旋翼的6-DOF动力学，并使用[49]中的公式用四元数表示它的姿态。这个问题的状态维数为n = 12和m = 4，表示四旋翼的全状态和PWM电机指令。最大的问题是动态避障场景，该场景在高频上解决，由316个决策变量、248个线性等式约束和172个线性不等式约束组成。

2)评估——8字轨迹跟踪：我们比较了TinyMPC和其他控制器的跟踪性能，如图4所示。对于较快的轨迹，最大速度和姿态偏差分别达到1.5 m/s和20◦。只有TinyMPC可以在尊重执行器限制的同时跟踪整个参考，而梅林格和布雷斯西亚尼尼的控制器几乎立即崩溃。TinyMPC在最多7次迭代时间内的所有步骤中收敛，并在由500 Hz控制频率定义的2 ms求解时间下收敛。

3)评估——极端的初始姿态：图1（底部）显示了裂缝在以90◦姿态误差初始化时的性能。TinyMPC在考虑输入限制的情况下，显示出了最佳的恢复性能，最大位置误差为23 cm。PID和Brescianini控制器的最大误差分别为40 cm和65 cm，同时违反了输入限制（图5）。其他控制器，INDI和梅林格，未能稳定四旋翼，导致它坠毁

4)评估——动态障碍避免：我们展示了TinyMPC通过避免移动棒来处理时变状态约束的能力（图1顶部）。这些实验更具挑战性，因为约束在非活动和活动之间任意切换，需要更多的迭代来解决收敛。在每个MPC步骤中，障碍物球的更新位置被重新线性化，允许无人机避免摆动棒的非计划性移动。如图所示，四旋翼可以在空间中自由移动，以避免动态障碍，并安全地回到悬停位置。作为一个额外的挑战，我们添加了一个约束，这样四旋翼必须保持在一个由x = 0定义的垂直平面内。在成功地避开动态障碍的同时，最大偏离了大约5厘米。

6 结论

我们介绍了TinyMPC，一种用于资源受限嵌入式系统的模型预测控制求解器。与现有的最先进的解决方案（如OSQP）相比，TinyMPC使用ADMM来处理状态和输入约束，同时利用MPC问题的结构和LQR的见解来减少内存占用并加快在线执行。我们展示了TinyMPC在Crazyflie纳米四旋翼机上的实际性能，该四旋翼飞机在输入和障碍物限制下执行高动态任务。

未来工作的几个方向仍然存在。首先，扩展TinyMPC以处理二阶圆锥约束应该是很简单的，这在许多MPC应用中对于推力和摩擦建模是有用的。我们还计划通过开发定点版本来进一步减少TinyMPC的硬件需求，因为许多小型微控制器缺乏硬件浮点支持。最后，为了便于部署和采用，我们计划用高级语言（如Julia或Python）为TinyMPC开发一个代码生成说唱歌手，类似于OSQP和CVXGEN。

有关更多信息和开始使用我们的开源解决方案，我们建议用户访问我们的网站，https://tinympc.org.